What is Linear System?
A linear system is a system that satisfies the superposition principle, which states that the response of a linear system to any input is the sum of the responses to each individual input. This means that if an input signal is multiplied by a constant and then applied to the system, the output of the system will also be multiplied by that same constant.
Linear systems are often used to model physical systems, such as electrical circuits, mechanical systems, and other systems that exhibit linear behavior. They are particularly useful because they can be analyzed using a variety of mathematical tools, such as Laplace transforms and Fourier series, which allow us to understand their behavior in detail.
Linear systems can be represented using a mathematical model known as a linear differential equation, which describes how the system responds to an input signal. The solutions to these equations can be used to determine the output of the system for any given input.
Overall, linear systems are an important concept in the field of signals and systems because they provide a simple and powerful way to analyze and understand the behavior of a wide variety of physical systems.
What is Non-Linear System?
A nonlinear system is a system that does not satisfy the superposition principle, which states that the response of a linear system to any input is the sum of the responses to each individual input. This means that if an input signal is multiplied by a constant and then applied to the system, the output of the system will not necessarily be multiplied by that same constant.
Nonlinear systems are often used to model physical systems that exhibit complex or nonlinear behavior, such as chemical reactions, biological systems, and certain types of electronic circuits. These systems can be difficult to analyze using traditional mathematical techniques because they do not exhibit the same kind of simple, predictable behavior as linear systems.
Nonlinear systems can be represented using a mathematical model known as a nonlinear differential equation, which describes how the system responds to an input signal. Solving these equations can be challenging, as they may not have closed-form solutions and may require the use of numerical methods.
Overall, nonlinear systems are an important concept in the field of signals and systems because they are prevalent in the real world and can exhibit a wide range of complex and interesting behaviors.
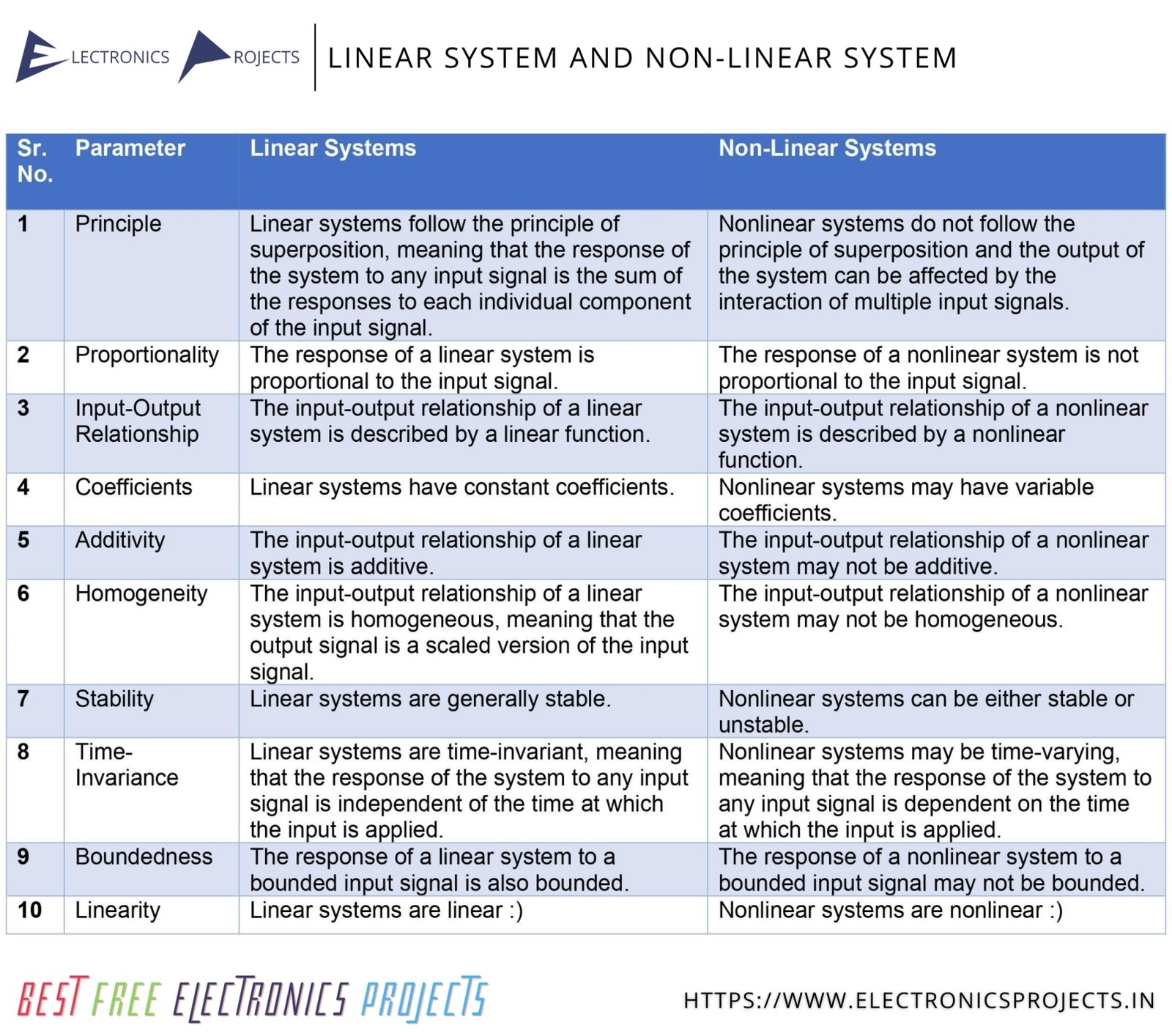
Difference between Linear and Non-Linear System:
Text Version:
| SR. NO. | PARAMETER | LINEAR SYSTEM | NON-LINEAR SYSTEM |
|---|---|---|---|
| 1 | Explanation | Linear systems follow the principle of superposition, meaning that the response of the system to any input signal is the sum of the responses to each individual component of the input signal. | Nonlinear systems do not follow the principle of superposition and the output of the system can be affected by the interaction of multiple input signals. |
| 2 | Proportionality | The response of a linear system is proportional to the input signal. | The response of a nonlinear system is not proportional to the input signal. |
| 3 | Input-Output Relationship | The input-output relationship of a linear system is described by a linear function. | The input-output relationship of a nonlinear system is described by a nonlinear function. |
| 4 | Coefficients | Linear systems have constant coefficients. | Nonlinear systems may have variable coefficients. |
| 5 | Additivity | The input-output relationship of a linear system is additive. | The input-output relationship of a nonlinear system may not be additive. |
| 6 | Homogeneity | The input-output relationship of a linear system is homogeneous, meaning that the output signal is a scaled version of the input signal. | The input-output relationship of a nonlinear system may not be homogeneous. |
| 7 | Stability | Linear systems are generally stable. | Nonlinear systems can be either stable or unstable. |
| 8 | Time Invariance | Linear systems are time-invariant, meaning that the response of the system to any input signal is independent of the time at which the input is applied. | Nonlinear systems may be time-varying, meaning that the response of the system to any input signal is dependent on the time at which the input is applied. |
| 9 | Boundedness | The response of a linear system to a bounded input signal is also bounded. | The response of a nonlinear system to a bounded input signal may not be bounded. |
| 10 | Linearity | Linear systems are linear 🙂 | Nonlinear systems are nonlinear 🙂 |
Image Version:
Download above image in HD | Size: 800 KB | JPG Image
