What is Invertible System?

In signals and systems, an invertible system is a system that has a unique output for every input. This means that if we know the input signal x(t) and the output signal y(t) of the system, we can determine the system’s response uniquely.

In other words, if we have two different input signals x1(t) and x2(t) that produce the same output signal y(t), then the system is not invertible. On the other hand, if every input signal x(t) produces a unique output signal y(t), then the system is invertible.

Invertibility is an important property of systems because it allows us to determine the input signal given the output signal. This can be useful in many applications, such as filtering or signal processing, where we want to remove certain components of an input signal or extract certain features of the signal.

Invertibility is also related to the concept of causality. A causal system is invertible if and only if it is stable, which means that the output of the system does not grow indefinitely as time goes on. On the other hand, a non-causal system is always invertible, because the output can depend on future input values as well as past and present input values.

What is Non-Invertible System?

In signals and systems, a non-invertible system is a system that does not have a unique output for every input. This means that if we know the input signal x(t) and the output signal y(t) of the system, we cannot determine the system’s response uniquely.

In other words, if there are two different input signals x1(t) and x2(t) that produce the same output signal y(t), then the system is non-invertible. On the other hand, if every input signal x(t) produces a unique output signal y(t), then the system is invertible.

Non-invertibility is an important property of systems because it means that we cannot determine the input signal given the output signal. This can be a limitation in certain applications, such as filtering or signal processing, where we want to remove certain components of an input signal or extract certain features of the signal.

Difference between Invertible and Non-Invertible System:

Text Version:

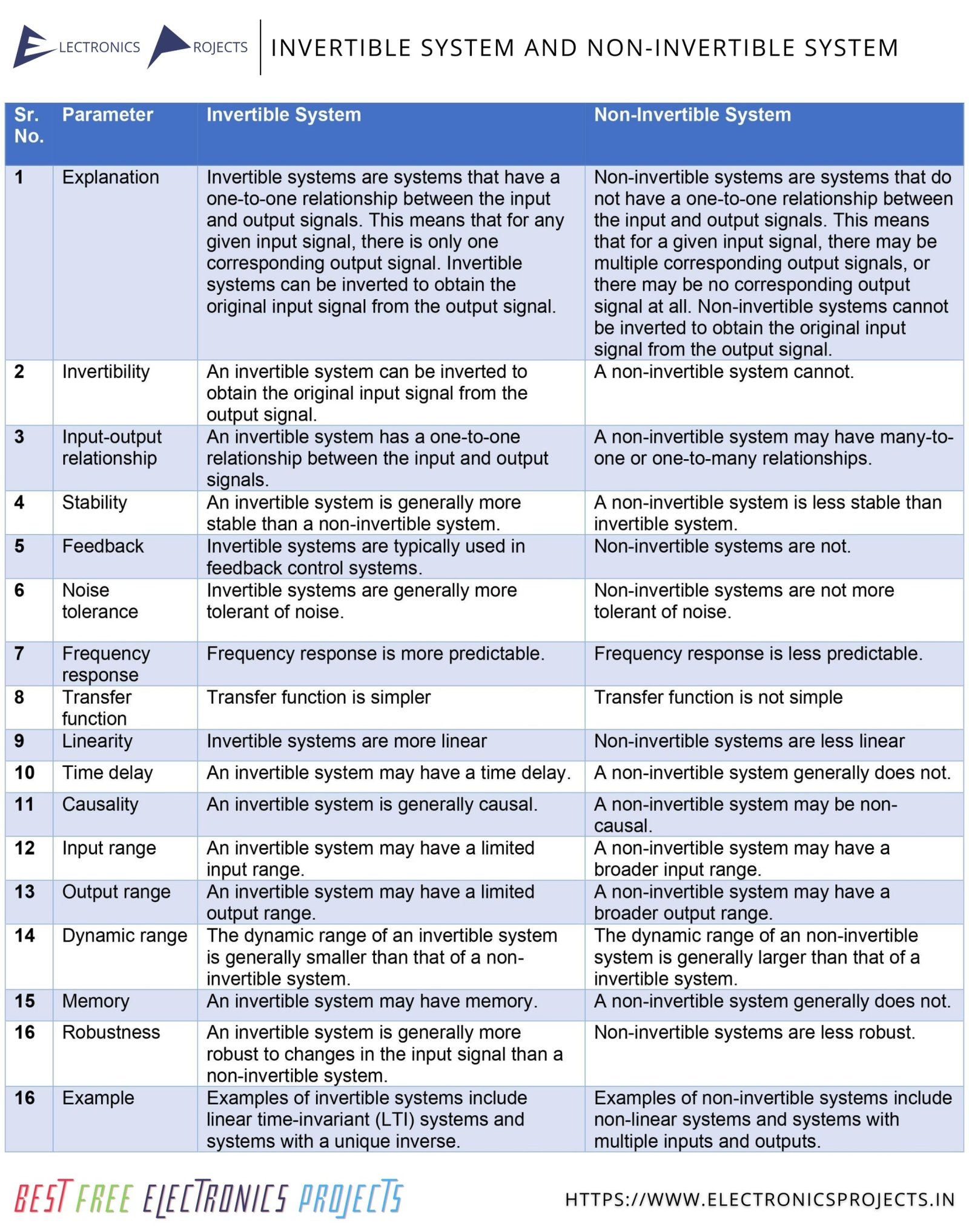
SR. NO.	PARAMETER	INVERTIBLE SYSTEM	NON-INVERTIBLE SYSTEM
1	Explanation	Invertible systems are systems that have a one-to-one relationship between the input and output signals. This means that for any given input signal, there is only one corresponding output signal. Invertible systems can be inverted to obtain the original input signal from the output signal.	Non-invertible systems are systems that do not have a one-to-one relationship between the input and output signals. This means that for a given input signal, there may be multiple corresponding output signals, or there may be no corresponding output signal at all. Non-invertible systems cannot be inverted to obtain the original input signal from the output signal.
2	Invertibility	An invertible system can be inverted to obtain the original input signal from the output signal.	A non-invertible system cannot.
3	Input-Output Relationship	An invertible system has a one-to-one relationship between the input and output signals.	A non-invertible system may have many-to-one or one-to-many relationships.
4	Stability	An invertible system is generally more stable than a non-invertible system.	A non-invertible system is less stable than invertible system.
5	Feedback	Invertible systems are typically used in feedback control systems.	Non-invertible systems are not.
6	Noise tolerance	Invertible systems are generally more tolerant of noise.	Non-invertible systems are not more tolerant of noise.
7	Frequency response	Frequency response is more predictable.	Frequency response is less predictable.
8	Transfer function	Transfer function is simple	Transfer function is not simple
9	Linearity	Invertible systems are more linear	Non-invertible systems are less linear
10	Time delay	An invertible system may have a time delay.	A non-invertible system generally does not.
11	Causality	An invertible system is generally causal.	A non-invertible system may be non-causal.
12	Input range	An invertible system may have a limited input range.	A non-invertible system may have a broader input range.
13	Output range	An invertible system may have a limited output range.	A non-invertible system may have a broader output range.
14	Dynamic range	The dynamic range of an invertible system is generally smaller than that of a non-invertible system.	The dynamic range of an non-invertible system is generally larger than that of a invertible system.
15	Memory	An invertible system may have memory.	A non-invertible system generally does not.
16	Robustness	An invertible system is generally more robust to changes in the input signal than a non-invertible system.	Non-invertible systems are less robust.
17	Example	Examples of invertible systems include linear time-invariant (LTI) systems and systems with a unique inverse.	Examples of non-invertible systems include non-linear systems and systems with multiple inputs and outputs.

Image Version:

Download above image in HD | Size: 1 MB | JPG Image

More: