
Table of Contents
Introduction
In the realm of wireless communication, the efficient utilization of the limited radio frequency spectrum is of paramount importance. With the growing demand for wireless services, Cognitive Radio (CR) technology has emerged as a promising solution to address the spectrum scarcity challenge. One of the key components of CR is spectrum utilization, which involves the effective allocation and management of available spectrum resources.
Understanding Spectrum Utilization
Spectrum utilization refers to the process of optimizing the usage of the radio frequency spectrum. Traditionally, spectrum allocation has been based on static and exclusive assignments, leading to underutilization of spectrum resources. Cognitive Radio, on the other hand, enables dynamic spectrum access by allowing unlicensed users to opportunistically access underutilized portions of the spectrum.
The need for spectrum utilization arises from the fact that a significant portion of the spectrum remains underutilized or even unused at any given time and location. By employing spectrum utilization techniques, CR systems can efficiently exploit these idle frequencies, thereby enhancing overall spectrum efficiency.
The Bayesian Method in Spectrum Utilization
The Bayesian method is a statistical approach used in spectrum sensing, a crucial aspect of spectrum utilization in Cognitive Radio. Spectrum sensing involves detecting the presence or absence of primary users in a specific frequency band. The Bayesian method leverages statistical inference to make optimal decisions regarding spectrum utilization.
Developed in the 18th century by Thomas Bayes, the Bayesian method provides a mathematical framework for updating beliefs or probabilities based on new evidence. In the context of spectrum sensing, the Bayesian method allows CR devices to estimate the presence or absence of primary users by iteratively updating the probabilities based on observed signal characteristics.
Working of Spectrum Sensing and Utilization using Bayesian Method
In Cognitive Radio systems, spectrum sensing is performed to detect primary users and identify available spectrum opportunities. The Bayesian method enhances spectrum sensing accuracy by incorporating prior knowledge about the probability distribution of primary user signals.
The working of spectrum sensing and utilization using the Bayesian method can be summarized in the following steps:
- Initialization: The Bayesian method starts with an initial belief or prior probability distribution of the presence of primary users in the spectrum.
- Observation: The CR device samples the received signal and extracts relevant features for spectrum sensing.
- Update: Using the observed features, the Bayesian method updates the belief or posterior probability distribution based on Bayes’ theorem.
- Decision: The CR device makes a decision on the presence or absence of primary users by thresholding the posterior probability distribution.
- Utilization: If primary users are detected, the CR device opportunistically accesses the available spectrum for transmission.
Comparison between Bayesian Method and Other Methods
To better understand the advantages of the Bayesian method in spectrum utilization, let’s compare it with other commonly used methods:
| Method | Advantages | Disadvantages |
|---|---|---|
| Energy Detection | Simple implementation | Less reliable in low signal-to-noise ratio (SNR) scenarios |
| Matched Filtering | High detection accuracy | Requires prior knowledge of primary user signals |
| Cyclostationary Feature Detection | Effective in non-Gaussian noise environments | Complex computational requirements |
| Bayesian Method | Utilizes prior knowledge to improve detection accuracy | Requires accurate prior probability distribution estimation |
Pros and Cons of Bayesian Method
The Bayesian method offers several advantages in spectrum utilization:
- Improved detection accuracy by incorporating prior knowledge
- Flexibility in adapting to changing signal characteristics
- Effective utilization of spectrum resources by reducing false alarms and missed detections
However, there are a few limitations to consider:
- Accurate estimation of the prior probability distribution is crucial
- Computational complexity may increase with the number of observed features
Implementing Bayesian Method for BPSK Signal in MATLAB Software
1. Bayesian Method for BPSK Signal MATLAB Code:
% Bayesian Method for BPSK Signal
% Parameters
num_samples = 5000;
SNR_dB_range = -20:0.5:20;
% BPSK modulation
data = randi([0,1], 1, num_samples);
bpsk_signal = 2 * data - 1;
% Initialize arrays to store results
error_rate = zeros(size(SNR_dB_range));
estimated_bits = zeros(1, num_samples);
% Simulation loop
for snr_index = 1:length(SNR_dB_range)
% Add AWGN
snr = 10^(SNR_dB_range(snr_index)/10);
noise_power = 1 / snr;
noise = sqrt(noise_power) * randn(1, num_samples);
received_signal = bpsk_signal + noise;
% Bayesian detection
estimated_bits = (received_signal > 0);
% Calculate error rate
error_rate(snr_index) = sum(estimated_bits ~= data) / num_samples;
end
% Plot results in a semilog graph
figure;
semilogy(SNR_dB_range, error_rate, 'o-', 'LineWidth', 2);
grid on;
title('Bayesian Method for BPSK Signal');
xlabel('SNR (dB)');
ylabel('Error Rate');
Output:

2. Bayesian Method for Detection Probability and False Alarm Probability:
% Bayesian Method for BPSK Signal with Performance Metrics(Detection Probability and False Alarm Probility
% Parameters
num_samples = 5000;
SNR_dB_range = -20:0.5:20;
% BPSK modulation
data = randi([0,1], 1, num_samples);
bpsk_signal = 2 * data - 1;
% Initialize arrays to store results
error_rate = zeros(size(SNR_dB_range));
detection_probability = zeros(size(SNR_dB_range));
false_alarm_rate = zeros(size(SNR_dB_range));
% Simulation loop
for snr_index = 1:length(SNR_dB_range)
% Add AWGN
snr = 10^(SNR_dB_range(snr_index)/10);
noise_power = 1 / snr;
noise = sqrt(noise_power) * randn(1, num_samples);
received_signal = bpsk_signal + noise;
% Bayesian detection
estimated_bits = (received_signal > 0);
% Calculate performance metrics
error_rate(snr_index) = sum(estimated_bits ~= data) / num_samples;
detection_probability(snr_index) = sum(estimated_bits & data) / sum(data);
false_alarm_rate(snr_index) = sum(estimated_bits & ~data) / sum(~data);
end
% Plot results in a semilog graph
figure;
subplot(2,1,1);
semilogy(SNR_dB_range, error_rate, 'o-', 'LineWidth', 2);
grid on;
title('Bayesian Method for BPSK Signal');
xlabel('SNR (dB)');
ylabel('Error Rate');
subplot(2,1,2);
plot(SNR_dB_range, detection_probability, 'o-', 'LineWidth', 2, 'DisplayName', 'Detection Probability');
hold on;
plot(SNR_dB_range, false_alarm_rate, 's-', 'LineWidth', 2, 'DisplayName', 'False Alarm Rate');
grid on;
title('Performance Metrics');
xlabel('SNR (dB)');
ylabel('Probability');
legend('Location', 'Best');Output:

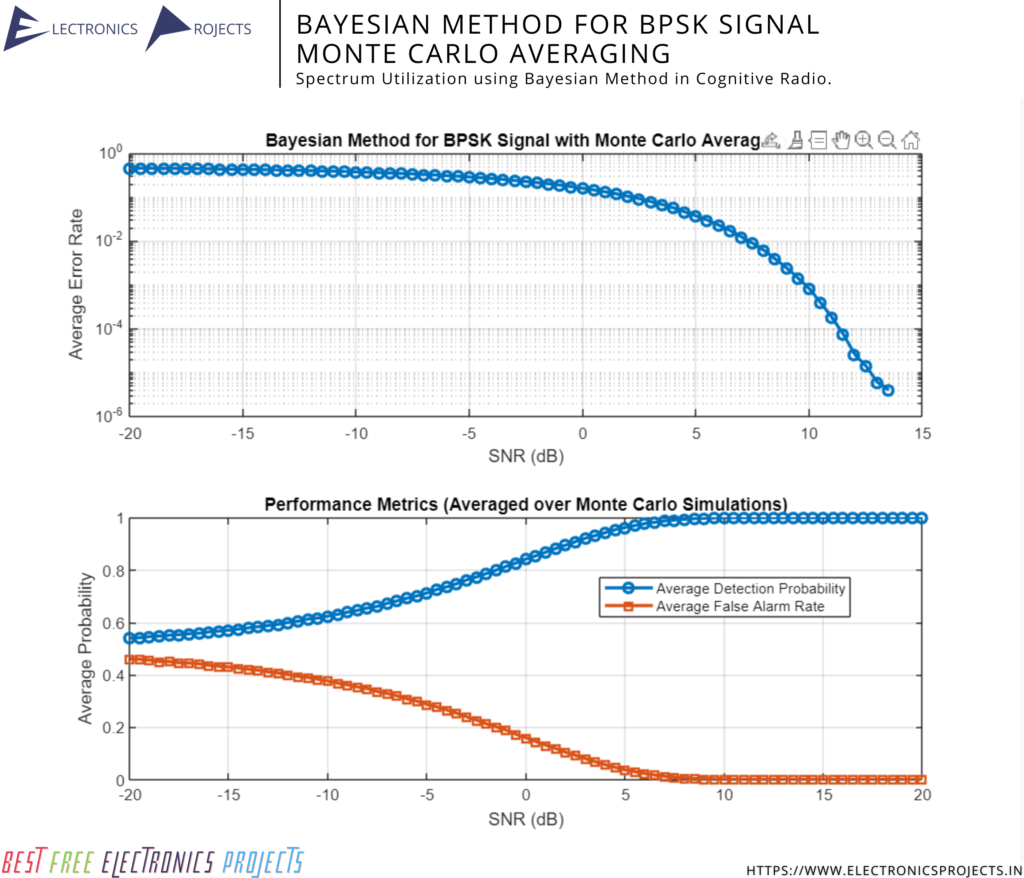
3. Bayesian Method for Monte Carlo Averaging with Detection Probability and False Alarm Probability:
% Bayesian Method for BPSK Signal with Monte Carlo Averaging
% Parameters
num_samples = 5000;
SNR_dB_range = -20:0.5:20;
num_simulations = 100; % Number of Monte Carlo simulations
% Initialize arrays to store results
error_rate_avg = zeros(size(SNR_dB_range));
detection_probability_avg = zeros(size(SNR_dB_range));
false_alarm_rate_avg = zeros(size(SNR_dB_range));
% Monte Carlo simulation loop
for sim = 1:num_simulations
% BPSK modulation
data = randi([0,1], 1, num_samples);
bpsk_signal = 2 * data - 1;
% Simulation loop
for snr_index = 1:length(SNR_dB_range)
% Add AWGN
snr = 10^(SNR_dB_range(snr_index)/10);
noise_power = 1 / snr;
noise = sqrt(noise_power) * randn(1, num_samples);
received_signal = bpsk_signal + noise;
% Bayesian detection
estimated_bits = (received_signal > 0);
% Calculate performance metrics for each simulation
error_rate(sim, snr_index) = sum(estimated_bits ~= data) / num_samples;
detection_probability(sim, snr_index) = sum(estimated_bits & data) / sum(data);
false_alarm_rate(sim, snr_index) = sum(estimated_bits & ~data) / sum(~data);
end
end
% Average results over simulations
error_rate_avg = mean(error_rate, 1);
detection_probability_avg = mean(detection_probability, 1);
false_alarm_rate_avg = mean(false_alarm_rate, 1);
% Plot results in a semilog graph
figure;
subplot(2,1,1);
semilogy(SNR_dB_range, error_rate_avg, 'o-', 'LineWidth', 2);
grid on;
title('Bayesian Method for BPSK Signal with Monte Carlo Averaging');
xlabel('SNR (dB)');
ylabel('Average Error Rate');
subplot(2,1,2);
plot(SNR_dB_range, detection_probability_avg, 'o-', 'LineWidth', 2, 'DisplayName', 'Average Detection Probability');
hold on;
plot(SNR_dB_range, false_alarm_rate_avg, 's-', 'LineWidth', 2, 'DisplayName', 'Average False Alarm Rate');
grid on;
title('Performance Metrics (Averaged over Monte Carlo Simulations)');
xlabel('SNR (dB)');
ylabel('Average Probability');
legend('Location', 'Best');
Output:
4. Bayesian Method Vs Energy Detection in Cognitive Radio:
% Comparison of Energy Detection and Bayesian Method for Detection Probability
% Parameters
num_samples = 5000;
SNR_dB_range = -20:0.5:20;
num_simulations = 100; % Number of Monte Carlo simulations
% Initialize arrays to store results for Bayesian Method
detection_probability_avg_bayesian = zeros(size(SNR_dB_range));
% Initialize arrays to store results for Energy Detection
detection_probability_avg_energy = zeros(size(SNR_dB_range));
% Monte Carlo simulation loop for Bayesian Method
for sim = 1:num_simulations
% BPSK modulation
data = randi([0,1], 1, num_samples);
bpsk_signal = 2 * data - 1;
% Simulation loop
for snr_index = 1:length(SNR_dB_range)
% Add AWGN for Bayesian Method
snr = 10^(SNR_dB_range(snr_index)/10);
noise_power = 1 / snr;
noise = sqrt(noise_power) * randn(1, num_samples);
received_signal = bpsk_signal + noise;
% Bayesian detection
estimated_bits_bayesian = (received_signal > 0);
% Calculate performance metrics for each simulation (Bayesian Method)
detection_probability_avg_bayesian(sim, snr_index) = sum(estimated_bits_bayesian & data) / sum(data);
end
end
% Average results over simulations for Bayesian Method
detection_probability_avg_bayesian = mean(detection_probability_avg_bayesian, 1);
% Monte Carlo simulation loop for Energy Detection
for sim = 1:num_simulations
% BPSK modulation
data = randi([0,1], 1, num_samples);
bpsk_signal = 2 * data - 1;
% Simulation loop
for snr_index = 1:length(SNR_dB_range)
% Add AWGN for Energy Detection
snr = 10^(SNR_dB_range(snr_index)/10);
noise_power = 1 / snr;
noise = sqrt(noise_power) * randn(1, num_samples);
received_signal_energy = abs(bpsk_signal + noise).^2;
% Set a threshold for energy detection (adjust as needed)
threshold_energy = 0.5;
% Energy detection
estimated_bits_energy = (received_signal_energy > threshold_energy);
% Calculate performance metrics for each simulation (Energy Detection)
detection_probability_avg_energy(sim, snr_index) = sum(estimated_bits_energy & data) / sum(data);
end
end
% Average results over simulations for Energy Detection
detection_probability_avg_energy = mean(detection_probability_avg_energy, 1);
% Plot results for Detection Probability
figure;
plot(SNR_dB_range, detection_probability_avg_bayesian, 'o-', 'LineWidth', 2, 'DisplayName', 'Bayesian Method');
hold on;
plot(SNR_dB_range, detection_probability_avg_energy, 's-', 'LineWidth', 2, 'DisplayName', 'Energy Detection');
grid on;
title('Comparison of Detection Probability');
xlabel('SNR (dB)');
ylabel('Probability');
legend('Location', 'Best');Output:

Applications of Spectrum Utilization using Bayesian Method
The utilization of spectrum resources using the Bayesian method finds applications in various domains:
- Wireless communication networks
- Internet of Things (IoT) systems
- Smart cities and infrastructure
- Satellite communication
- Emergency communication systems
By leveraging the Bayesian method, these applications can improve spectrum efficiency, enhance communication reliability, and enable seamless connectivity in dynamic and heterogeneous environments.
