What is Continuous Time Signal?
In continuous time signals, the signal is defined over an uninterrupted range of time. This means that the signal can take on any value at any instant of time. An example of a continuous time signal is an analog audio signal, which can take on an infinite number of values within a certain range of amplitudes over time.
What is Discrete Time Signal?
Discrete time signals are defined only at specific, isolated points in time. The signal can only take on a value at these discrete points. An example of a discrete time signal is a sequence of digital audio samples, which are defined at specific points in time and are typically represented by a series of binary digits.
To understand better, here’s more info about Continuous and Discrete time signals: One of the key differences between continuous time signals and discrete time signals is that continuous time signals are generally more difficult to manipulate and analyze mathematically, due to the infinite number of possible values that they can take on. Discrete time signals, on the other hand, are much simpler to work with, as they are defined at specific points in time and can be represented by a finite series of discrete values.
Both continuous and discrete time signals can be processed and analyzed using mathematical techniques such as Fourier analysis, which allows us to represent the signal in terms of its frequency components. However, the techniques used for analysis may be different depending on whether the signal is continuous or discrete.
Diagram of Continuous Time Signal and Discrete Time Signal:
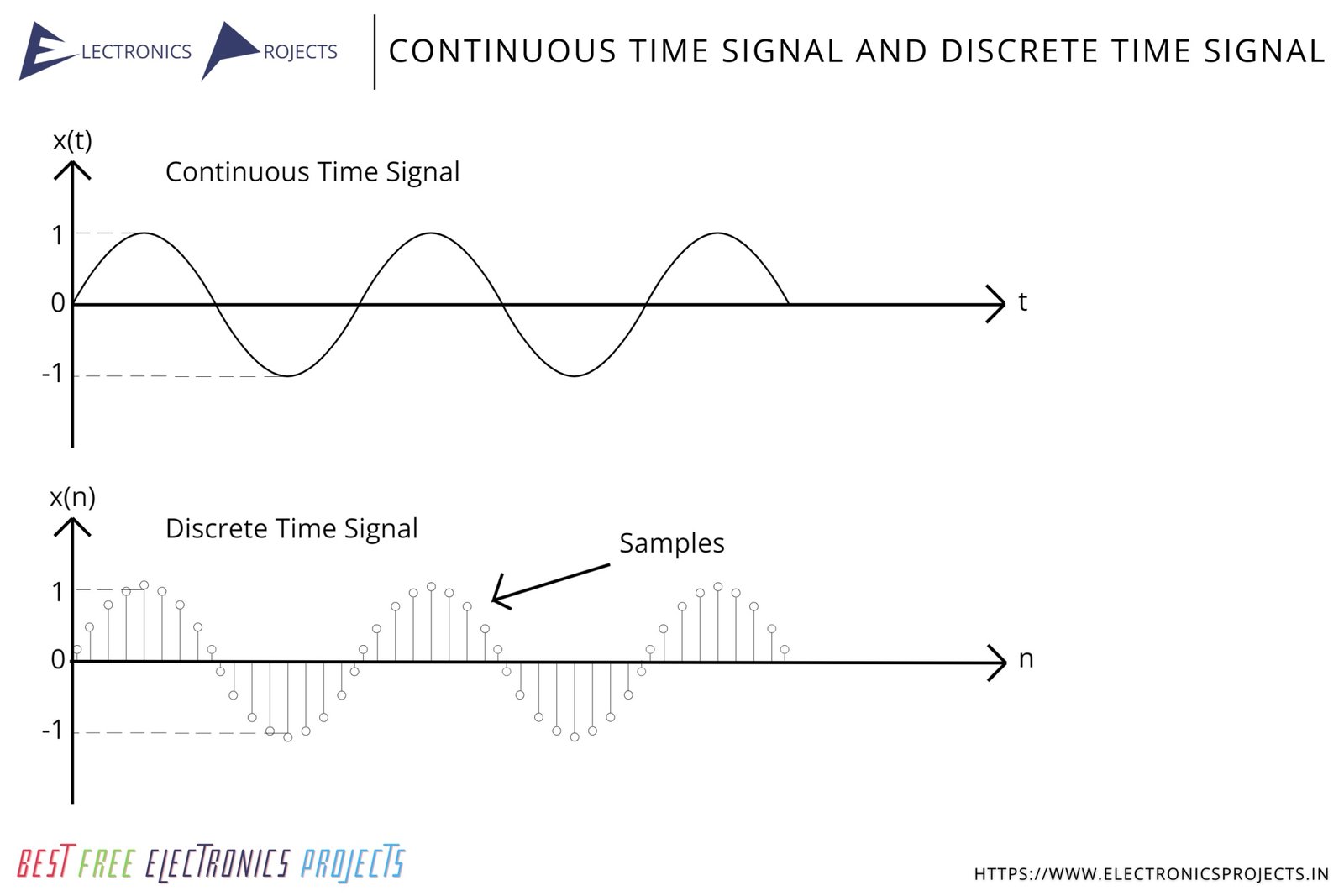
Download above image in HD | Size: 170 KB | JPG Image
Difference between Continuous Time Signal and Discrete Time Signal:
Text Version:
| SR. NO. | PARAMETER | CONTINUOUS TIME SIGNAL | DISCRETE TIME SIGNAL |
|---|---|---|---|
| 1 | Definition | Continuous time signals are functions of a continuous variable, such as time. | Discrete time signals are sequences of values that are defined at discrete, evenly spaced intervals of time. |
| 2 | Representation | Continuous time signals are typically represented using mathematical functions, such as sine or cosine waves. | Discrete time signals are usually represented using sequences of numbers. |
| 3 | Analysis | Continuous time signals can be analysed using continuous time domain techniques, such as Laplace transforms and Fourier transforms. | Discrete time signals can be analysed using discrete time domain techniques, such as z-transforms and discrete Fourier transforms. |
| 4 | Frequency | Continuous time signals have a continuous frequency spectrum. | Discrete time signals have a discrete frequency spectrum. |
| 5 | Digital Signal Processing | Continuous time signals, on the other hand, require analog-to-digital conversion before they can be processed digitally. | Discrete time signals are used extensively in digital signal processing, as they can be easily processed by computers. |
| 6 | Storage | Continuous time signals, on the other hand, require more storage space and cannot be transmitted digitally without first being sampled and quantized. | Discrete time signals can be easily stored and transmitted digitally, as they are represented by a series of numbers. |
| 7 | Bandwidth | Continuous time signals have an infinite bandwidth. | Discrete time signals have a finite bandwidth. |
| 8 | Modulation | Continuous time signals can be modulated using analog techniques, such as amplitude, frequency, and phase modulation. | Discrete time signals are typically modulated using digital techniques, such as pulse code modulation (PCM) and quadrature amplitude modulation (QAM). |
| 9 | Noise | Continuous time signals are more susceptible to noise and interference, as they are transmitted over analog channels. | Discrete time signals are less susceptible to noise, as they are transmitted digitally. |
| 10 | Filtering | Filtering of continuous time signals is typically done using analog filters. | Filtering of discrete time signals is typically done using digital filters. |
| 11 | Stability | Continuous time systems can be analysed using stability criteria such as the Routh-Hurwitz stability criterion and the Nyquist stability criterion. | Discrete time systems can be analysed using stability criteria such as the Jury stability criterion and the Hurwitz stability criterion. |
| 12 | Causality | Continuous time systems can be either causal or non-causal. | Discrete time systems are always causal. |
| 13 | Time Delay | Continuous time systems can have an arbitrary time delay. | Discrete time systems have a fixed time delay of one sample period. |
| 14 | Mathematical Operations | Continuous time signals can be manipulated using continuous time domain mathematical operations, such as integration and differentiation. | Discrete time signals can be manipulated using discrete time domain mathematical operations, such as discrete integration and discrete differentiation. |
Image Version:

Download above image in HD | Size: 1 MB | JPG Image
